MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Cours
Calcul différentiel et intégral (1)
Nous suivrons l'ordre des articles de Jacques Lefebvre : Moments et aspects de l'histoire du calcul différentiel et intégral, Bulletin AMQ, déc. 1995, mars, mai, octobre 1997, mars, mai 1998.
Ce premier cours portera sur les deux premiers articles.
Dans ce qui suit, la structure des articles sera présentée, mais des compléments viennent s'y ajouter.
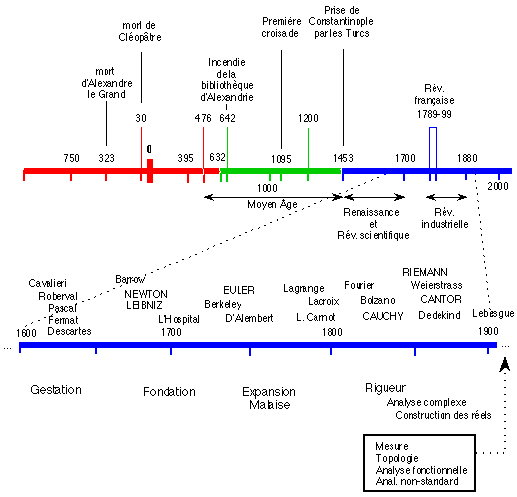
1. Une ligne du temps relié à l'évolution du calcul différentiel et intégral
2. Premier article : La Grèce
- Les quatre mots de l'expression consacrée : Calcul, différentiel, intégral, et.
- Thèmes généraux relatifs au calcul
différentiel et intégral
- Infiniment petit et infiniment grand
- Discret et continu
- Arithmétique - géométrie - algèbre (analyse)
- Nombre et figure (grandeur)
- Temps et espace
- Le fini et l'infini
- Les matériaux de base
- Problèmes générateurs : aire, tangente, vitesse, maximun-minimum, centre de gravité
- concepts de fondements
- Nombres et rapport
- Séries
- Limite
- Infiniment petit et infiniment grand
- Fonction
- L'antiquité grecque
- Deux types de difficultés avant Euclide
- Mesure des grandeur et rapport
- Crise des incommensurables
- L'infini
- Les paradoxes de Zénon d'Élée (490-425 av. notre ère) :l'infini est à éviter
- Mesure des grandeur et rapport
- Quatre ajustements en fonction de ces
difficultés
- Rejet de l'infini actuel
Un exemple, Archimède (287-212 av. notre ère)La Méthode relative aux théorèmes mécaniques
Rappel préliminaire Le principe du levier : Fd = F'd' ou F est à F' comme d' est à d.
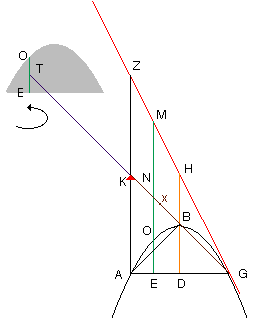
Énoncé Prop. 1)( : Soit AG la base d'une parabole. Trois fois le secteur de parabole ABG et quatre fois le triangle ABG ont la même aire, où AD = DG et BD est | | au diamètre de la parabole.
- Rejet de l'infini actuel
- La méthode d'exhaustion : éviter l'infini en
utilisant le raisonnement par l'absurde.
- Théorème d'exhaustion : Euclide Livre X,
proposition 1 (article de J. Lefebvre, p. 50):
Deux grandeurs inégales étant proposées, si l'on retranche de la plus grande une partie plus grande que sa moitié, et si l'on retranche du reste une partie plus grande que sa moitié, et si l'on fait toujours la même chose, il restera une certaine grandeur qui sera plus petite que la plus petite des grandeurs proposées.
- Propositions démontrées à l'aide de ce
théorème:
- Euclide, Livre XII, propositions 1
et 2
Prop. 1 : Les polygones semblables inscrits dans des cercles sont entr'eux comme les quarrés des diamètres
Prop. 2 : Les cercles sont entr'eux comme les quarrés de leurs diamètres
- Archimède : De la mesure du
cercle (Dhombre, J., et al., Mathématiques
au fil des âges, Paris : Gauthier-Villars, 1987,
p. 133)
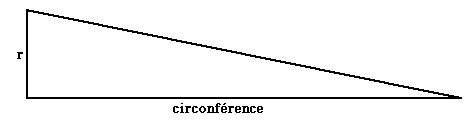
Énoncé (Prop. 1) Tout cercle est équivalent à un triangle rectangle dans lequel l'un des côtés de l'angle droit est égal au rayon du cercle et la base (c'est-à-dire l'autre côté de l'angle droit) égale au périmètre du cercle.
Structure de la démonstration :
Soit C, l'aire du cercle, et T, l'aire du triangle de base la circonférence c du cercle et de hauteur r, le rayon du cercle
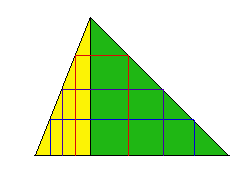
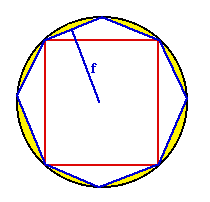
Supposons que C>T. Alors, je peux construire un polygone d'aire P, inscrit dans le cercle, tel que l'aire (en jaune dans la figure) comprise en le polygone et le cercle soit plus petite que C - T, autrement dit C - P < C - T. (J'utilise le théorème d'exhaustion, comme Euclide l'avait fait dans sa proposition 2 du livre 12). - Alors, on a que T < P.
- Or, l'aire P du polygone est égale à celle d'un triangle rectangle de hauteur f et de base le périmètre du polygone. Or on a que f < r et que le périmètre du polygone est inférieur à la circonférence c du cercle. Donc, P < T.
- Contradiction !
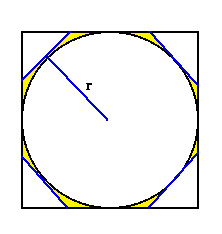
Supposons maintenant que T > C, Alors, je peux construire un polygone d'aire P, circonscrit au cercle, tel que l'aire (en jaune dans la figure) comprise entre le polygone et le cercle soit plus petite que T - C, autrement dit, P - C < T - C. (À nouveau par le théorème d'exhaustion) - Alors, on a que P < T.
- Or, l'aire P du polygone est égale à celle d'un triangle rectangle de hauteur f et de base le périmètre du polygone. Or on a que f = r et que le périmètre du polygone est supérieurà la circonférence c du cercle. Donc, T< P.
- Contradiction !
- Euclide, Livre XII, propositions 1
et 2
- Théorème d'exhaustion : Euclide Livre X,
proposition 1 (article de J. Lefebvre, p. 50):
Démonstration :
Soient GZ tangent à la parabole en G et AZ | | au diamètre.
1) Par des théorèmes sur les paraboles, on a DB = BH
Et donc l'aire du triangle AZG est égal à quatre (4) fois l'aire du triangle ABG.
2) Par un théorème sur les paraboles, si O est un point quelconque de la parabole, on a
ME est à EO comme GA est à AE (ME:EO :: GA:AE)
Par ailleurs, par les triangles semblables, GA est à AE comme GK est à KN (GA:AE ::GK:KN)
Donc, ME est à EO comme GK est à KN (ME:EO :: GK:KN) (Pensons au levier ici).
3) Prolongeons le segment GK au delà de K jusqu'à un point T tel que GK = KT.
On a alors, par le point 2), que ME est à EO comme KT est à KN.
4) On peut interpréter cette proportion, par le principe du levier, comme voulant dire que le segment OE placé à T équilibre le segment ME placé à N, avec pour pignon le point K.
5) Prenant alors successivement tous les points "O" de la parabole délimitant le secteur et considérant que le secteur ABG est composé des segments "OE" accolés les uns aux autres et que le triangle AZG est de même composés des segments "ME" accolés les uns aux autres, on peut dire que le secteur ABG placé à T, perpendiculaire au plan du secteur (donc perpendiculaire à l'écran) équilibre le triangle AZG, autour du pignon K.
Autrement dit, si x est le centre de gravité du triangle AZG, on a que le triangle AZG est au secteur ABG comme TK est à Kx.
6) Or le centre de gravité du triangle AZG se trouve sur GK à un point x tel que Kx soit le tiers de GK. Il en résulte donc que le triangle AZG est au secteur ABG comme TK est au tiers de KG, autrement dit comme 3 est à 1. Donc le secteur ABG est trois fois plus petit que le triangle AZG. Or, comme on l'a dit en 1), le triangle AZG vaut quatre fois le triangle ABG. Il en découle que trois fois le secteur de parabole ABG correspond à la même aire que quatre fois le triangle ABG.
CQFD
Archimède ne considère pas cette approche comme une preuve acceptable, même si elle donne une idée du résultat cherché.
(Un mot sur les oeuvres d'Archimède et leur parcourt pour nous atteindre.)
On voit que le raisonnement dépend de la nature de la figure étudiée.
Remarquons aussi qu'Archimède donne l'équivalent d'une formule, alors qu'Euclide donne le sien en terme de rapport (Vision plus puriste que celle d'Archimède)
- Contourner les incommensurables - la théorie des rapports et proportions
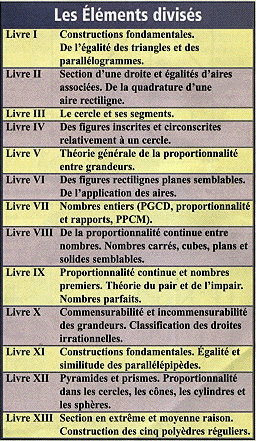
Un regard sur la structure des Éléments d'Euclide
- Structure des Éléments
.
Tiré de l'article de Bernard Vitrac, Les treize Livres d'Euclide, dans Les Cahiers de Science & Vie, Mathématiques, Ce que les Grecs ont vraiment inventé, no 55, Février 2000, p. 50 à 56.
Un site intéressant : Les Éléments, avec une vision "géométrique" avec des couleur (signalé par Fernando Hitt) :
- La quatrième proportionnelle
Ce sera Descartes (1637) qui, justement, en utilisant la quatrième proportionnelle, et en fixant l'unité de mesure pour l'une des grandeurs, en vient à justifier clairement la multiplication comme une opération fermée sur les nombres (vus simplement comme mesures de longueurs). C'est là qu'on voit que les rapport ne sont pas des nombres pour les grecs.
- La notion de grandeur (non numérique) - la propriété d'Archimède
À l'époque d'Euclide, on discutait à savoir si les angles corniculaires étaient archimédiens (lorsque considérés comme des angles).
- De nombreuses réalisations
- Recherches de tangentes
- Euclide (Éléments, Livre III, déf. 2) : Une droite est dite toucher le cercle lorsque, rencontrant le cercle et étant produite, elle ne coupe pas le cercle.(Unetouchante, expression du XVIIe siècle)
- détermination de tangentes : Euclide (le cercle), Apollonius (coniques), Archimède (+ une direction du déplacement, Spirale d'Archimède)
- Optimisation : Apollonius (250-175 av. notre ère) Il montre par exemple comment tracer un segment de droite depuis un point quelconque jusqu’à une conique donnée de façon à ce que le segment soit, selon la position du point par rapport à la conique, le plus court ou le plus long. Il remarque alors qu’une perpendiculaire à ce segment passant par l’extrémité qui sur la conique est tangente à la conique.
- Recherches de tangentes
3. Deuxième article, Moyen Âge et dix-septième siècle avant Newton et Leibniz.
Le Moyen Âge
Les paradoxes sur l'infini
- Deux cercles concentriques ont le même nombre de points.
- La diagonale d'un carré a le même nombre de points que le côté du carré.
Oresme (1323-1382) et la latitude des formes
- Toute qualité uniformément difforme a même sujet ou un sujet égal selon le degré du point milieu de ce sujet.
- « En divisant ainsi le sujet en parties égales, et en désignant la plus petite partie comme la première, le rapport des qualités partielles, c'est-à-dire leur relation naturelle, est comme la série des nombres entiers impaires où le premier est 1, le deuxième 3, le troisième 5, etc., ce qui est évident sur la figure. » (Dhombre, J., et al., Mathématiques au fil des âges, Paris : Gauthier-Villars, 1987, p. 181)
- La série harmonique 1 + 1/2 + 1/3 + 1/4 + … + 1/i + …
Il remarque que pour i = n+1 à 2n, 1/i > 1/2n. Il prend alors le premier terme, 1, lui ajoute un minorant à la somme des deux termes suivants, 1/3 + 1/4 > 1/4 + 1/4 = 1/2 (n = 2) , puis de même pour les quatre termes suivants, 1/5 + 1/6 +1/7 + 1/8 > 4 x 1/8 = 1/2 (n = 4 = 22), etc. Chacune de ces sommes partielles est supérieure à 1/2 (pour n , 1/n+1 + ... + 1/2n > n x (1/2n) = 1/2). La série est donc minorée par kx1/2, avec k pouvant être aussi grand que l'on veut. La valeur de la somme est donc plus grande que n'importe quel nombre, aussi grand soit-il.
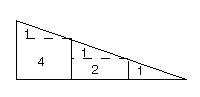
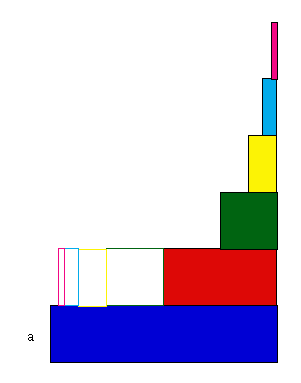
- « Si un certain temps avait été ainsi divisé en parties proportionnelles [c'est-à-dire la division successive par deux] ; qu'en la première partie de ce temps, un certain mobile se mût avec une certaine vitesse ; qu'en la seconde, il se mût deux fois plus vite, en la troisième trois fois plus vite, et ainsi de suite, la vitesse croissant toujours de même, la vitesse totale serait précisément quadruple de la vitesse de la première partie ; de sorte qu'en l'heure entière, ce mobile parcourrait un chemin exactement quadruple de celui qu'il a parcouru pendant la première partie de cette heure. »
La figure suivante explique le raisonnement d'Oresme (sans lien de couleurs entre les deux figures)
devient
- Les précurseurs de Newton et Leibniz
Est-ce un pur hasard si le calcul s'est développé au XVIIe siècle ?
Étude du mouvement : Astronomie physique, la navigation, la balistique.
- Détermination de la trajectoire d'un projectile : Vitesse et accélération
- Tangentes : l'optique
- Maxima et minima : Balistique, astronomie (périhélie, aphélie), optique (trajet de la lumière)
- Mesure des longueurs, Aires : Astronomie (distance parcourue par une planète), centre de gravité, forces d'attractions entre deux corps.
- Galilée (1564-1642)
- Les paradoxes reliés à l'infini
- La roue d'Aristote
- L'anneau et le cercle
- L'arc de cercle qui devient une droite (à l'infini)
L'étude du mouvement(Discours concernant deux nouvelles sciences, 1638)
- Le temps pendant lequel un espace quelconque est franchi par un mobile, partant du repos avec un mouvement uniformément accéléré, est égal au temps pendant lequel le même espace serait franchi par le même mobile avec un mouvement uniforme, dont le degré de vitesse serait la moitié du plus grand et dernier degré de vitesse atteint au cours du mouvement uniformément accéléré. [On sent l'esprit d'Oresme ici]
- Si un mobile, partant du repos, tombe avec un mouvement uniforme accéléré, les espaces parcourus en des temps quelconques par ce même mobile sont entre eux en raison double des temps, c'est-à-dire comme les carrés de ces mêmes temps. (Cette raison double (le carré du temps) vient de ce que les espaces se calculent par la somme des nombres impairs, qui est le carré du temps)
- Cavalieri
(1598-1647) Geometria
indivisibilibus (1635)
La surface comme une juxtaposition de lignes.[Struick, D.J., A Source Book in Mathematics, 1200-1800, Cambridge, Mass. : Harvard Univ. Press, 1969, pp. 214-219.)
- Terminologie : o.l.a signifie omnis
lineae a, ou toutes les lignes a, ou la "somme" des
lignes de a. Pour la "somme" des carrés, il emploie o.q.a,
et pour les cubes, o.c.a .
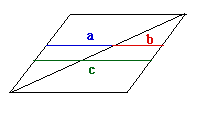
- Dans un parallélogramme on a que Sc = 2Sa, ou S symbolise "somme" (ma notation). Sa signifie "Somme des a"
- Il démontre aussi que Sc2 = 3Sa2
- Voyons la preuve pour Sc3 = 4Sa3 (avec ces notations et non celles de Cavalieri)
- Terminologie : o.l.a signifie omnis
lineae a, ou toutes les lignes a, ou la "somme" des
lignes de a. Pour la "somme" des carrés, il emploie o.q.a,
et pour les cubes, o.c.a .
On a que (x+y)3 = x3 + 3x2y + 3xy2 + y3. Or, comme c = a + b, à chaque ligne horizontale, on a
Sc3 = Sa3 + 3Sa2b + 3Sab2 + Sb3.
Par symétrie entre les a et les b, on obtient Sc3 = 2Sa3 + 6Sa2b. (*)
Or, Sc3 =c Sc2 = c S(a+b)2 = c(Sa2 + 2Sab + Sb2) ; et Sa2 = Sb2 = (1/3)Sc2 [par un résultat précédant].
D'où, Sc3 = (2/3)cSc2 + 2cSab
= (2/3)Sc3 + 2(a+b)Sab
= (2/3)Sc3 + 2Sa2b + 2Sb2a
= (2/3)Sc3 + 4Sa2b.
Donc, Sc3 = 12 Sa2b.
En utilisant cette dernière identité dans l'équation (*), on obtient Sc3 = 2Sa3 +(1/2)Sc3, d'où,
Sc3 = 4Sa3.
- On retrouve là une formule connue...
- Le contre-exemple de Guldin (1577-1643)
Selon le principe de Cavalieri, les segments de droites à comparer doivent être parallèles. Il en est ainsi dans le cas suivant. Les triangles jaunes et vert sont, selon Cavalieri, égaux.
- Roberval
(1602-1675)
- La tangente à la parabole
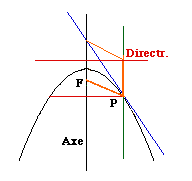
Un point P appartient à la parabole de foyer P et d'une directrice donnée, si la distance de P au foyer est égale à la distance à la directrice. (Dans le figure les segments donnant ces distances sont orange et épais.) La direction de la tangente est donné par le parallélogramme déterminé par ces segments, puisque si FP croit d'une certaine longueur, la distance à la directrice croit de cette même longueur.
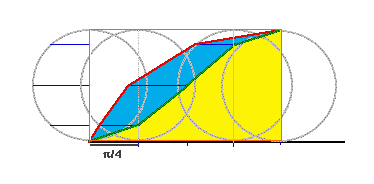
(Figure tracée pour quatre points seulement)
- Considérons un cercle de rayon r. La Cycloïde est le tracé fait par le point du cercle qui au départ est en contact avec le segment plancher.
- La courbe verte, dite compagnon de la cycloïde (au-dessus de la partie en jaune), qui en fait est la courbe de (1-cos), divise en deux partie égales le rectangle orange (par la symétrie de sa construction). Or rectangle orange a une aire de circonférence x diamètre, donc rPi x 2r. Donc la partie jaune a une aire de r2Pi, soit l'aire du cercle.
- La partie en bleu (dont la frontière supérieure, en rouge, est la cycloïde) a une aire égale à celle du demi-cercle, car elle est faite successivement des segments (bleus) allant du diamètre à la circonférence.
- Donc l'aire sous la cycloïde est égale une fois et demi l'aire du cercle.
- Descartes
(1596-1650) La tangente, par un cercle tangent à la courbe.
(Katz, Victor, History of Mathematics, p. 472-473)
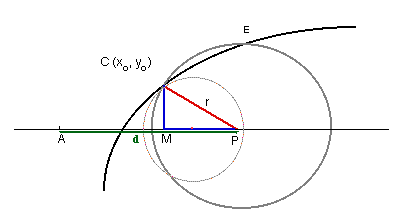
En étudiant un cercle de rayon donné passant par un point P d'une courbe, Descartes constate que le cercle coupera en un autre point cette courbe, sauf si le rayon du cercle passant par P est perpendiculaireà la courbe. Alors, dans ce dernier cas, le cercle ne coupe qu'en un seul point la courbe. Ainsi, pour déterminer une perpendiculaireà une courbe en un point P(x0,y0) de cette courbe, il faut faire en sorte que le centre du cercle soit placé de façon telle que ce cercle ne coupe la courbe qu'en un seul point. En exprimant cela algébriquement, il s'agit de résoudre un système d'équations, provenant de l'égalité des coefficients dans l'égalité de l'ordonnée d'un point du cercle et d'un point de la courbe, de façon à ce que ce système n'ait qu'une solution (pour x = x0). En général, cela exige des calculs très longs et parfois difficiles.
Soit le centre du cercle. Soit A l'origine du système de coordonnées. La courbe a pour équation y = f(x). On veut trouver la tangente en C à cette courbe.
L'équation du cercle de centre P est y2 = r2 - (d-x)2. Les points communs au cercle et à la courbe satisfont donc l'équation (égalité en y) f2(x) - r2 + (d-x)2 = 0. De plus, il faut qu'il n'y ait qu'une seule racine, celle-ci double. L'expression de gauche est dès lors divisible par (x-x0)2. Donc, on a qu'il existe un polynôme q(x) tel que f2(x) - r2 + (d-x)2 = (x-x0)2q(x). En égalant les coefficients, on obtient un système d'équations dont r et d sont les inconnues (en fait d et r sont dépendant l'un de l'autre). En résolvant ce système, on trouve les valeurs qui nous permettent de déterminer la position du centre P. Voici un exemple (dans Katz mais non dans Descartes).
Trouver la tangente à y = x2 au point (x0,x0). On a que
(x2)2 - r2 + (d-x)2 = (x-x0)2q(x).
Dès lors, q(x) est un polynôme de degré 2 qui a la forme x2 + ax + b. En remplaçant dans la formule ci-haut et en égalant les coefficients des puissances correspondantes de chaque côté de l'égalité, on obtient le système suivant
a - 2x0 = 0 (coefficients des termes de degré 3)
b - 2x0a + x02 = 1 (coefficients des termes de degré 2)
ax02 - 2bx0 = -2d (coefficients des termes de degré 1)
bx02 = d2 - r2 (les termes constants)
En déterminant la valeur de a, par la première équation, puis, en remplaçant dans la seconde, déterminant la valeur de b, on peut déterminer la valeur de d en utilisant la troisième. La position de P est ainsi fixée (2x03 + x0, 0). On peut dès lors calculer la pente du rayon PC : -y0/(d-x0) = -x02/2x03 = -1/2x0. La pente de la tangente est donc 2x0, ce qui correspond au résultat connu.
- Fermat
(1601-1665) La tangente par les infiniment petits
- Dans son étude sur la mesure des volume de vin dans les tonneaux (1615), Kepler remarque que le cube est le volume maximal d'un parallélépipède inscrit dans une sphère est le cube. À l'occasion de cette étude , il remarque que près d'un maximum, la variation est pour ainsi dire imperceptible.
- La méthode du maximum et du minimum
- Faire p(x1) = p(x2)
- Diviser par x1 - x2
- Poser x1 = x2
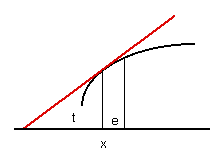
- Faire p(x) ˜ p(x+e) (Adéquation, non pas = )
- Diviser par e
- Poser e= 0
Trouver l'aire maximale d'un quadrilatère de périmètre donné
B+H = a. Posons x = B, alors H = a-x. Aire = x(a-x) = ax - x2.
(Première méthode) Méthode de la racine double
Or, Viète avait montré que que dans cette équation, le coefficient a était la somme des deux racines de la façon suivante: Si x1 et x2 sont les racines, alors : (ax1 - x12)/(x1 - x2) = (ax2 - x22)/(x1 - x2). Doù b = x1 + x2.
Fermat remarque que le maximum est atteint lorsqu'il y a une racine double : x = b/2.
Il propose alors la méthode suivante pour trouver le fax de p(x):
Exercice : le faire pour p(x) = bx2 - x3.
(Deuxième méthode) Méthode des infinitésimaux.
Remplacer x1 et x2 de la première méthode par x et e, ou e = x1 - x2.
La méthode devient :
Faire en sorte que M = x(a-x) ait une racine double
(Suite)
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |